Zastosowanie informatyki w przedsiębiorstwie handlowym - lab. z programu Excel 2007
Wydział Zarządzania, WZ, UTP, Bydgoszcz
=========================================================
=========================================================
=========================================================
W tym zadaniu musimy rozwiązać problem transportowy związany z przewiezieniem towaru z różnych magazynów do różnych sklepów, tzw. problem dystrybucji.
W Excelu musimy obliczyć ile sztuk i do jakich sklepów ma być przewieziony towar z danego magazynu, tak aby koszty były najniższe. Oznacza to, że nie będziemy wysyłać towaru z Rzeszowa do Bydgoszczy, ale za to prześlemy go z Olsztyna, bo stamtąd jest bliżej, a co za tym idzie taniej. Może być jednak tak, że część towaru do Bydgoszczy zostanie przesłane z Łodzi, a część z Olsztyna, dodatkowo Łódź prześle jeszcze towar do Warszawy i Poznania. Ale wszystko okaże się podczas obliczeń.
Ważna informacja
Za transport płacimy 0,52 złote za kilometr za sztukę.
Czyli jeśli w samochodzie jest jeden towar to za kilometr płacimy 0,52 zł, ale jeśli są w nim 3 produkty to za ten sam kilometr płacimy już 1,56 zł.
Najpierw przepisujemy polecenie i wprowadzamy komórkę z kosztami transportu za 1 km.
Teraz uzupełniamy tabelę numer 1, 2 i 3.
Tabela 1 to odległości wyrażone w kilometrach pomiędzy poszczególnymi dostawcami, a odbiorcami.
Tabela 2 pokazuje ile sztuk towaru potrzebuje dany sklep.
Tabela 3 przedstawia ile sztuk produktu może maksymalnie dostarczyć dany magazyn.
Jak widać zapotrzebowanie (891 sztuk) jest mniejsze od możliwości dostawców (1009 sztuk) także dla każdego towaru wystarczy :)
Polecenie 1
| Opracuj plan przewozu z Magazynów do Sklepów tak, aby łączne koszty transportu były minimalne. |
Tabela 4
Przedstawia ona koszt przewozu 1 sztuki produktu z magazynu do sklepu dla wszystkich możliwych kombinacji przejazdów.
Aby ją uzupełnić musimy przemnożyć wszystkie komórki z tabeli 1 i koszt transportu za kilometr (0,52 zł). Formuła dla mojego arkusza: =B10*$F$3, gdzie $F$3 to komórka ceny za transport za 1 km.
Następnie tą formułę przenosimy do pozostałych komórek tabeli, a w formie uzupełnionej wygląda tak:
Tabela 5
Zawiera ona plan transportu, czyli obliczone jakie ilości z danego magazynu należy wysłać do jednego z czterech sklepów. Oczywiście może tak być, że sklep otrzymuje towar tylko od jednego dostawcy albo od wszystkich po kilka sztuk. Wszystko obliczy solver.
Na razie przepisujemy tabele do Excel'a, jako wartości domyślne wpisujemy na razie "10". W kolumnie "Suma" (G41 - G44) będą zsumowane ilości towaru dostarczone do danego sklepu z różnych magazynów, np. dla wiersza "41" mamy zsumowane wszystkie produkty jakie dotarły do Bydgoszczy z poszczególnych magazynów. Formuła wygląda tak: "=SUMA(B41:F41)" i kopiujemy ją do kolejnych wierszy.
Sumujemy także liczby w danej kolumnie. Ich wartości będą w wierszu "45" o nazwie "Suma". Przykładowa formuła to: "=SUMA(B41:B44)". Kopiujemy ją do kolejnych kolumn.
Kolumna "Zapotrzebowanie" to ilość towaru jaką potrzebuje dany sklep. Wartości bierzemy z tabeli 2, ale ich nie przepisujemy, tylko robimy odniesienie: np. komórka "i41" zawiera formułę "=B17" podobnie czynimy dla pozostałych trzech komórek. Po obliczeniach musi się ona równać temu co znajduje się dwie kolumny na lewo, czyli temu co obliczy nam solver. Jeśli liczby się nie zgadzają to coś zrobiliśmy źle.
Wiersz "Dostawa" to ilość towaru jaką może wydać/wysłać dany magazyn. Obliczone wartości w wierszu "45" muszą być mniejsze/równe tym liczbom.
Podobnie jak poprzednio tworzymy odniesienia, a nie przepisujemy poszczególne wartości, czyli np. komórka "B47" zawiera formułę "=F17". Podobnie czynimy dla kolejnych pięciu pól.
Obliczanie przy pomocy Solver'a
Zanim przystąpimy do obliczeń i zanim przepiszemy tabelę 6 tworzymy sobie komórkę o adresie "i58", która będzie zawierać podliczony, całkowity koszt transportu.
W tej komórce będzie nowa formuła - "suma iloczynów". Co ona oznacza?
Przykładowo mamy dwie tabele o wymiarach 3x3.
Formuła ta służy do przemnożenia odpowiadających sobie pól, a następnie zsumowanie wszystkich wyników, czyli A1*A1' + A2*A2' + A3*A3' + B1*B1' + B2*B2' + B3*B3' + C1*C1' + C2*C2' + C3*C3'.
Dla naszego przykładu mnożymy tabele 4 i 5 (ale zaznaczamy tylko wartości, a nie nazwy). Formuła wygląda następująco: "=SUMA.ILOCZYNÓW(B32:F35;B41:F44)". Wychodzi nam 29 868,80 zł.
Teraz odpalamy Solver'a.
Komórką celu jest "i58", "Równa" ustawiamy na "Min", komórki zmienne to te z tabeli 5.
Warunki są trzy:
- liczba przewiezionych sztuk musi być wartością całkowitą
- obliczona ilość sztuk dla każdego sklepu musi się zgadzać z wartością zapotrzebowania
- obliczona ilość sztuk wysłana z danego magazynu musi by mniejsza lub równa możliwościom dostawcy
Zanim klikniemy "Rozwiąż" musimy wejść jeszcze w opcje Solver'a i zaznaczyć:
- Przyjmij model liniowy
- Przyjmij nieujemne
Klikamy OK, Rozwiąż i OK i w tabeli 5 mamy następujące wyniki:
Koszty transportu wyniosły 89 038,56 zł.
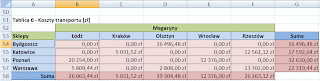
Tabela 6
Przedstawia koszty transportu wyliczonych przed chwilą towarów z konkretnego magazynu do konkretnego sklepu, np. koszt przewiezienia jednej sztuki z Olsztyna do Bydgoszczy wynosi 107,12 zł a sztuk tych musimy przewieźć 154, więc koszt transportu to 107,12*154 = 16 496,48 zł dla tej trasy.
Aby dokonać obliczeń musimy przemnożyć odpowiednie komórki z tabeli 4 i 5, czyli wchodzimy do komórki "B54" w tabeli 6 i wpisujemy "=ILOCZYN(B32;B41)". Formułę przenosimy do pozostałych 19 komórek. Gotowa tabela wygląda tak:
Polecenie 2
Mamy tu obliczyć ile tras/kursów wykona samochód dla obliczonych ilości towaru z tabeli 5, jeśli auto to ma określoną ładowność. Dla naszego zadania to 12 sztuk.
Tutaj musimy skorzystać z formuły, która zaokrągli obliczone w tej tabeli wartości do pierwszej większej liczby całkowitej, czyli 12,1 do 13; 14,7 do 15 itd.
Jest to spowodowane tym, że jeśli samochód ma ładowność na 12 sztuk produktu, a musi ich przewieźć
np. 30 to robi dwa kursy załadowany do pełna po 12 sztuk oraz jeden z 6-ma sztukami, co daje łącznie 3 kursy.
Formuła wygląda tak: "=ZAOKR.W.GÓRĘ(B41/$I$64;1)"
W nawiasie mamy dzielenie odpowiadającej komórki z tabeli numer 5 przez ładowność samochodu, przy czym adres komórki z ładownością nie może się zmieniać przy przenoszeniu formuły, stąd $$. Po średniku mamy 1, oznacza to zaokrąglanie jedności.
Gotowa tabela wygląda tak:
Możemy porobić dodatkowo sumę każdego wiersza i kolumny.
Komórka "i72" to suma wszystkich przejazdów, czyli "=SUMA(G72:G75)". Wyszło ich 78.
Dodatkowo (po ściągnięciu pliku Excela możecie wykasować)
Komórka "i76" to łączna ilość kilometrów jakie pokonają samochody dostarczając nam towar, dotyczą one tylko tej części trasy, za którą płacimy.
Jest to suma iloczynów tabeli 1 i 7. Formuła jaką zawiera to: "=SUMA.ILOCZYNÓW(B72:F75;B10:F13)"
Plik do pobrania:
Pobierz
Koniec